| Diese Seite hat Schule gemacht:
Rund ums Fliegen
Und hier sind wir bei der UNI München: http://www.leifiphysik.de/themenbereiche/allgemeines-gasgesetz/lb/heimversuche-mit-heissluft-bau-heissluftballon http://www.edugroup.at/fileadmin/DAM/Dateien/Praxis/Filmerziehung/Lepel/ab10b.pdf
|
|
Bauanleitung für einen Heißluftballon

|
Mit dem Programm kann man die Form und die Anzahl der benötigten Segmente berechnen. Das Programm gibt auch an, mit welcher "Tragkraft" bei einer Temperaturdifferenz z.B. 100 °C zu rechnen ist.
Zum Bau braucht man mehrere Bögen Seidenpapier, einen Kartonstreifen und Klebstoff. Ferner etwas Zeitungspapier, um das Zusammenkleben zu vereinfachen.
Nach dem Erstellen eines Schnittmusters, wird das Seidenpapier in entsprechende Bahnen zusammen geklebt. Für einen Ballon mit einem Radius von ca. 40 cm reichen sechs Segmente aus. Falte die Seidenpapierblätter in der Mitte und zeichne nun die Form des Ballons auf und schneide die Bahnen aus. (Ca. einen Zentimeter als Kleberand zugeben.) Klebe jedes Teil an der Kante mit dem darauffolgenden zusammen. Damit sie nicht wo anders ankleben zwischen die Bahnen Zeitungspapier legen. Klebe die erste Bahn mit der letzten zusammen, und der Ballon ist geschlossen. Nun erst einmal gut trocknen lassen. Die Hülle vorsichtig von links auf rechts umziehen, so kommen die Klebenähte nach Innen.
Mit einem Föhn heiße Luft einblasen. |

Nach einer Stunde Bauzeit und Kosten von ca. 5.- Euro "fährt"
der Indoor-Heißluftballon geheizt von einem Föhn durch das Wohnzimmer,
unter dem Beifall der Kinder.
Weitere Bilder des Heißluftballons
|
die Anzahl der Segmente:
|
die Temperaturdifferenz °C:
|
|
|
|
|
Gesamtlänge der Bahn cm:
Teillängen (l) cm:
|
|
0 Wert cm:
A Wert cm: B Wert cm: C Wert cm: D Wert cm: E Wert cm:
G Wert cm: |
|
Gesamtvolumen cm3 |
|
|
Gesamtoberfläche cm2 |
|
|
Volumendifferenz bei °C cm3 |
|
|
Gesamtauftrieb g |
|
Die Idee
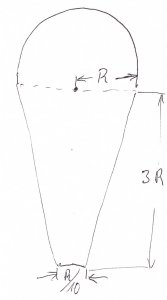
Da immer wieder nach der Formel zur Berechnung des Heißluftballons gefragt wird, stelle ich hier unsere Überlegungen kurz da: Die Idee war es, einen einfachen Heißluftballon (z.B. aus Seidenpapier) zu bauen. Um eine Vorstellung bezüglich des Auftriebes zu bekommen und um Schnittmuster für alle Größen generieren zu können, haben wir einen Ballon konstruiert, der aus einer Halbkugel und einem Kegelstumpf besteht. Der Überschaubarkeit halber, ist die Höhe des Kegelstumpfes gleich drei mal der Radius. Der kleine Radius ist ein Zehntel R. Somit wird der gesamte Ballon über den Radius definiert. Dar aus folgt: Oberfläche = 2 * Pi * R * R + Pi * 3*R * (R + R/10) und für das Volumen = 2/3 * Pi * R*R*R+R * Pi * (R*R + R*(R/10) + (R/10)*(R/10)) Mit Hilfe der Oberfläche kann nun das Gewicht des Heißluftballons errechnet werden. Das Gewicht pro Fläche des Hüllenmaterials mal der Oberfläche des Ballons ergibt das Gewicht der Ballonhülle.
Aus dem Volumen kann der Auftrieb berechnet werden. Hierfür benötigt man die Temperaturdifferenz zwischen der Luft im Ballon und der Luft außerhalb. Die Multiplikation des Volumens mit einer Konstanten und der Temperaturdifferenz ergibt den Auftrieb. Hierbei handelt es sich nur um eine theoretische Größe, denn die Luft ist nicht im gesamten Ballon gleich heiß und auch die Umgebungsluft weist Schwankungen auf. Mit diesen Berechnungen kann man jedoch bestimmen, wie groß ein Ballon aus einem bestimmten Material sein muss, um überhaupt vom Boden abheben zu können, wenn er beheizt wird. Weiterhin viel Spaß beim Heißluftballonbauen und natürlich auch beim Rechnen. Auf Fotos von eueren Ballons, weitere Anregungen und Anmerkungen sind wir gespannt. Formelsammlung:
Pi = 3.141592654
Geschichte und Funktionsweise des Heißluftballons
Anfang Juni 1783 sorgten die Brüder Jacques und Charles Montgolfier für großes Aufsehen: Sie füllten einen Ballon mit "stinkigem Rauch", der beim Verbrennen von Schafwolle und Stroh entstand. Und tatsächlich - der Ballon erhob sich in die Lüfte. Warum er aufstieg, konnte aber zunächst niemand erklären.
Eine Kommission von Wissenschaftlern beauftragte deshalb den Pariser Physik-Professor Jaques Charles, den Ballonflug genauer zu untersuchen.
Auch Charles wusste nicht, dass es bei den Montgolfieren (oder Heißluftballonen) nur auf die heiße Luft im Inneren ankommt.
Das Steigen und Sinken des Heissluftballons hängt von der Dichte des Gases im Inneren des Ballons ab. Je wärmer das Gas ist, desto niedriger ist die Dichte, dadurch verliert der Ballon an Gewichtskraft, und kann auf Grund der Auftriebskraft steigen. Wenn das Gas aber wieder abkühlt, erhöht sich die Dichte, die Gewichtskraft steigt und der Ballon sinkt.
Links zu anderen Seiten mit Bauanleitungen! http://www.almeschule.de/wb/pages/infos-aus-der-schule/projekte/modell-heissluftballon-projekt.php http://www.ballonfahren.de/modell_bauen_31__1.html http://www.meik.ch/Schule/Heissluftballon.asp http://www.funiculaire.de/beerfurth/pro11_hl.htm
Dr. Gerhard Nübel © 2000-2015 |